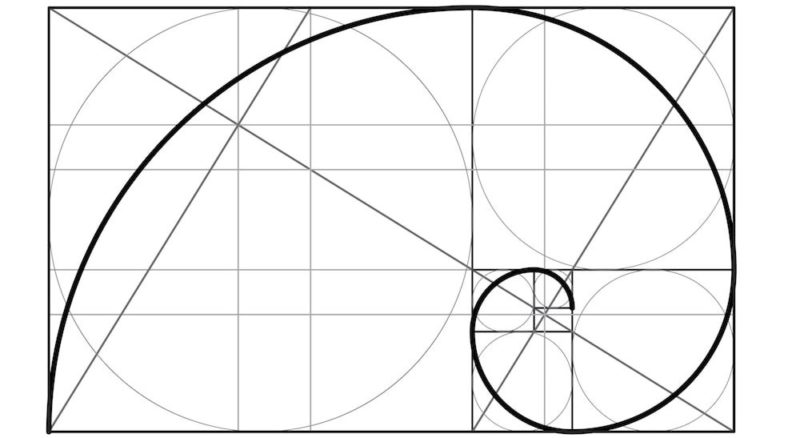
Proporción Áurea
Fue descubierta en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.
Video: ¿Qué es la Proporción Áurea?
Para comprender qué es la proporción áurea, hace falta primero entender el número áureo, un número algebraico irracional, representado con la letra griega phi (ϕ) en honor al escultor griego Fidias (500-431 a. C.), aunque a veces también con tau (Τ) o incluso con alfa minúscula (α), equivalente a 1,618033988749894… y a (1 + √5) / 2.
Este número posee propiedades matemáticas interesantes y fue descubierto en la Antigüedad, pero no como una expresión aritmética, sino geométrica: se trata de la relación o proporción que hay entre dos segmentos de una recta a y b, que cumplen con la ecuación algebraica:
(a + b) / a = a / b.
A esa relación se le llama la proporción áurea.
Historia de la Proporción Áurea
Según algunas interpretaciones de los descubrimientos arqueológicos, en las culturas mesopotámicas del 2000 a. C. existen ya evidencias de uso de la proporción áurea, a pesar de que no existe documentación previa a la Antigua Grecia en la que se hable de ello.
Los primeros estudios formales del número áureo pertenecen al filósofo Euclides (c. 300-265 a. C.), en su libro Los elementos, donde se demuestra que se trata de un número irracional, y algunos otros se le atribuyen al propio Platón (c. 428-347 a. C.).
En 1509, el teólogo y matemático italiano Luca Pacioli (c. 1445-1517) sugirió la conexión divina de dicho número en su De divina proportione (“Sobre la divina proporción”). Pacioli alegaba que estaba definido por tres segmentos de recta como la Divina Trinidad, que era inabarcable en su totalidad como Dios, y presentaba otras características interpretables como metáfora de lo sagrado.
Influenciado sin duda por esta idea, el artista del renacimiento alemán Alberto Durero (1471-1528) diseñó en 1525 la espiral áurea, después llamada “espiral de Durero”: el artista describió cómo trazar con regla y compás una espiral áurea basada en la proporción divina.
Hay otras referencias a la proporción áurea en las obras de Johannes Kepler (1571-1630) y Martin Ohm (1792-1872), siendo este último quien acuñó el nombre de la “sección áurea” en 1835. Sin embargo, hay evidencia de que el nombre era de uso común ya en esa época.
Desde entonces se le representó con la letra griega tau, hasta que en 1900 el matemático Mark Barr lo sustituyó por phi, como homenaje al escultor griego Fidias.
Analizaremos la proporción áurea en la obra de Salvador Dalí.
TP 7 - Proporción Áurea
Consigna: dibujar sobre una hoja A5, orientación horizontal el marco reglamentario (1 x 1 x 1 x 2 cm en la base). Pegar la etiqueta de la asignatura, centrada en la base.
Al dorso de la hoja copiar: N° TP, Título, Consigna, Fecha de Entrega y Rúbrica de evaluación.
Realizar un diseño propio luego y pintar con lápices de colores o de modo acromático (según elección).
Materiales: hoja N°5, regla, goma, compás, lápiz 2B, lápices de colores / negro.
Aquí presentamos algunos ejemplos: